❤ 1Gari Génération procédurale d'un donjon à la Zelda
Cet article explique comment générer à partir d'un algorithme simple des donjons comme ceux que l'on peut trouver dans Zelda Link's Awakening :
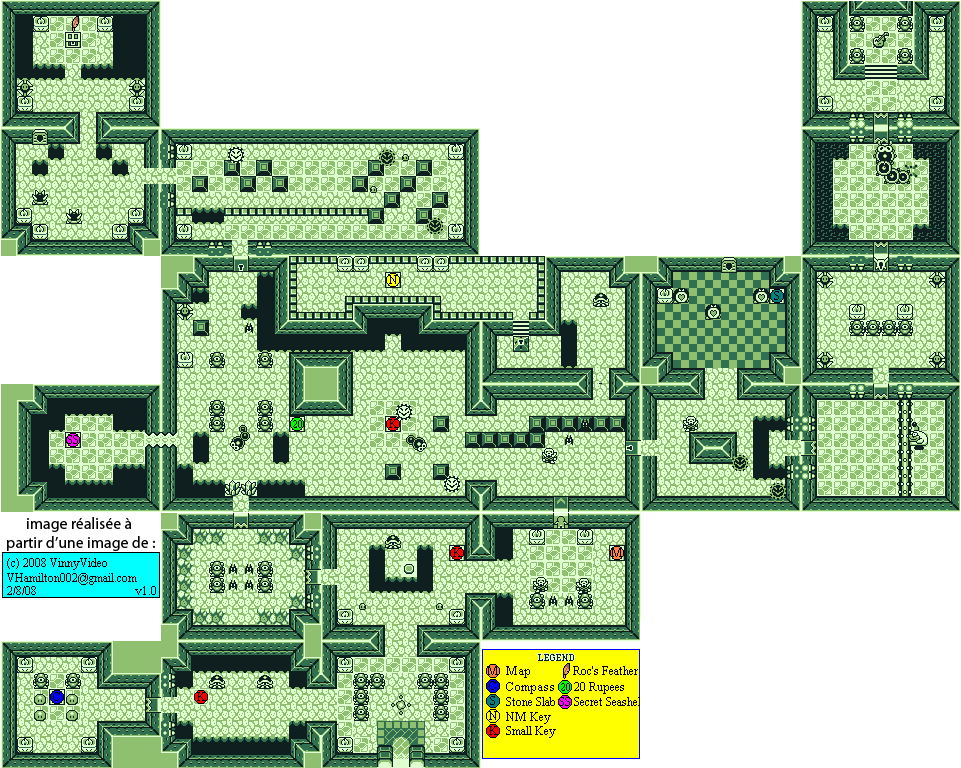
Rappels terminologiques
Je rappelle le sens de quelques termes que j'emploie, au cas où tout le monde ne serait pas familier avec :
Un graphe est un ensemble de points (appelés noeuds) reliés entre eux par des segments (appelés arêtes).
Pour qu'un graphe soit un "arbre", il ne faut pas qu'il comporte un cycle (une boucle).
Une extrémité de l'arbre est parfois appelée feuille. C'est un point qui n'a qu'une arête.
Affine signifie en ligne droite, c'est-à-dire selon une fonction du type y=a*x+b.
On appelle "arbre binaire" un arbre dont chaque noeud a un père (noeud contigu) et deux fils (noeuds contigus aussi), sauf un noeud qui n'a pas de père (appelé racine) et quelques noeuds qui n'ont pas de fils (appelés feuilles).
Présentation de l'algorithme
Le donjon est un ensemble de salles, reliées entre elles par des portes. Il s'agit donc d'un graphe : les salles sont les noeuds et les portes sont les arêtes.
Afin de pouvoir placer les clés et les serrures, nous avons besoin dans un premier temps que le donjon n'ait pas de cycles. Les cycles seront rajoutés en dernier. Nous partons donc d'un arbre :
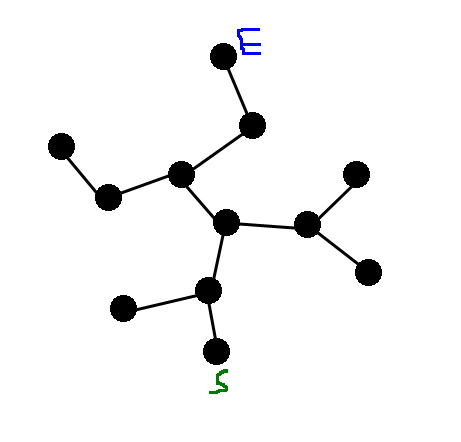
Notre donjon possède deux pôles : S (start) et E (end). On choisira la position de S de préférence à une extrémité de branche, et puis on choisira E de préférence à une extrémité et le plus loin possible de E.
Commençons à présent l'algorithme qui permet de placer les clés et les serrures.
On coupe le graphe en deux, de sorte que S soit d'un côté et E de l'autre :
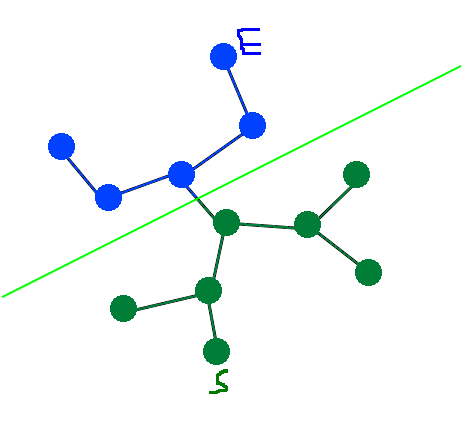
Nous allons placer à la limite un blocage : cela peut être une serrure, une porte fermée reliée à un interrupteur, une énigme qui nécessite l'arme du donjon...
Puis, dans la moitié du graphe qui contient S, il faudra placer l'objet résolvant : la clé, l'interrupteur qui ouvre la porte, l'arme du donjon...
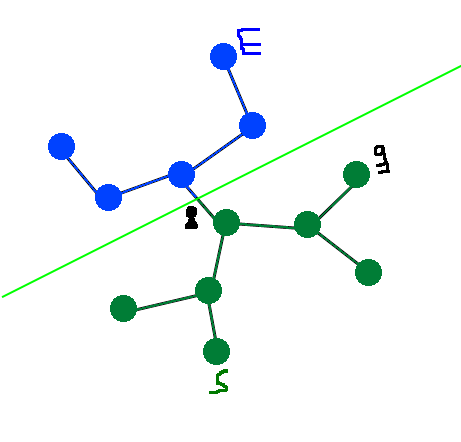
Il faudra aller chercher l'objet résolvant dans la première partie du donjon* pour pouvoir accéder à la deuxième partie.
L'idée est ensuite de recommencer cette division sur les deux moitiés obtenues !
La salle de l'objet résolvant devient E', et la salle juste après le blocage devient S' :
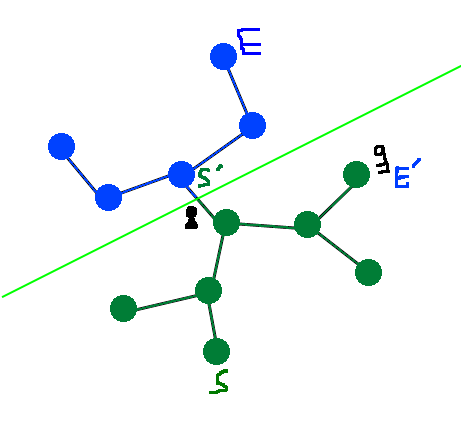
On re-divise récursivement :
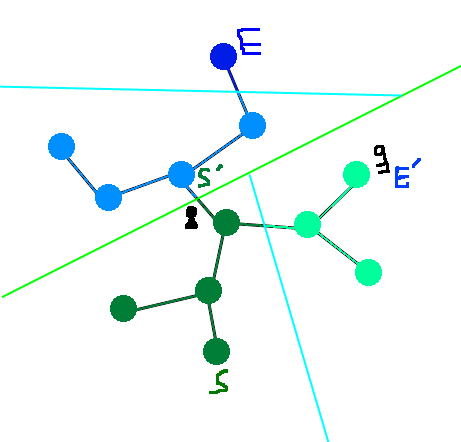
Et on ajoute les objets résolvants et les blocages correspondants.
Je conseille de mettre les objets résolvants aux extrémités si possible, afin d'éviter les branches entières de donjon inutiles.
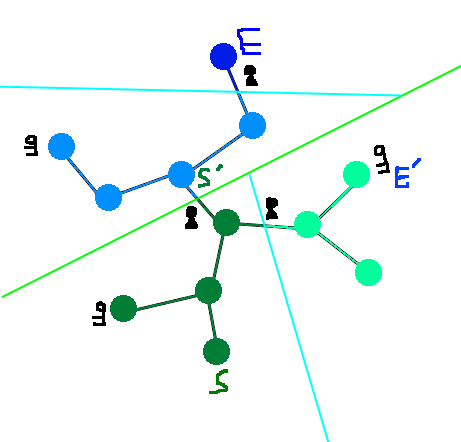
On a à présent un donjon valide (= forcément faisable).
Cet algorithme est récursif, je propose d'arrêter la division selon une fonction "probabilité de continuer". Si le bout de donjon dont on considère l'éventuelle division est petit (moins de 2 salles) on s'arrête forcément (probabilité 0). Si le bout de donjon est grand (plus de 6 salles) on le divise forcément (probabilité 1). Entre les deux on peut faire une probabilité affine ou bien juste mettre un nombre aléatoire qui vaut 0 ou 1.
Quelques remarques
La première division à effectuer doit être la serrure du boss (et son objet résolvant la clé du boss). Cette première division ne se fait pas n'importe où : elle doit se faire juste avant la dernière salle (E).
Les autres divisions peuvent se faire n'importe où sur le chemin allant de S à E.
Je conseille cependant après la division du boss de procéder à la division de l'arme du donjon, et de placer cette division à peu près au milieu du chemin allant de S à E.
Quand je dis "placer les objets résolvants en priorité à une extrémité", on peut se demander : comment savoir si une salle du donjon est une extrémité ?
C'est tout simplement une salle qui n'a qu'une seule porte.
Les objets facultatifs présents dans les donjons à la Zelda, comme par exemple la carte, la boussole ou des trésors bonus (argent, objet collectionnable...) peuvent être placés en priorité dans les extrémités inutilisées (par un objet résolvant) afin que ces salles soient utiles. Ensuite le reste de ces objets facultatifs peut être disséminé un peu partout.
Pour aller plus loin 1 : généralisation du placement des objets résolvants
Le lecteur attentif remarquera que la clé tout à gauche (dans la zone bleu clair) qui permet d'accéder à la zone bleu foncé aurait très bien pu être placée dans les zones vertes.
Qu'est-ce que cela signifie ?
Cela signifie que l'objet résolvant n'est pas forcément dans la moité inférieure de son bout de donjon, la seule chose qui importe c'est que l'objet résolvant soit avant son blocage.
Vu que la zone bleu clair est après la ligne verte, elle est après les zones vertes.
On doit placer l'objet résolvant dans une zone antérieure au blocage. Certes. La question qui se pose alors est : comment savoir si une zone du donjon est avant une autre ?
Modélisons notre découpage du donjon par un arbre binaire : la première division, celle qui coupe le donjon en deux, est la racine et les deux moitiés de donjon obtenues sont ses fils. Ensuite, vu qu'on divise chaque moitié, ces moitiés auront aussi deux fils, et cetera. Cet arbre contient donc toutes les zones du donjon à toutes les échelles possibles. Le fils gauche sera la partie avant le blocage et le fils droit la partie après le blocage.
Je propose alors une numérotation des zones :
- La racine possède pour valeur "2 puissance son altitude". Ici l'altitude est 2 donc sa valeur est 4.
- Quand un noeud obtient une valeur, il transmet sa valeur à son fils droit. On a maintenant trois noeuds avec la valeur 4.
- Pour un noeud sans valeur (le noeud n'est pas la racine et n'est pas le fils droit de son père) la valeur est la valeur du père (dont il est le fils gauche) moins 2 puissance l'altitude. On obtient donc 4-2^1=2 au milieu à gauche ; 2-2^0=1 en bas à gauche ; 4-2^0=3 en bas au milieu.
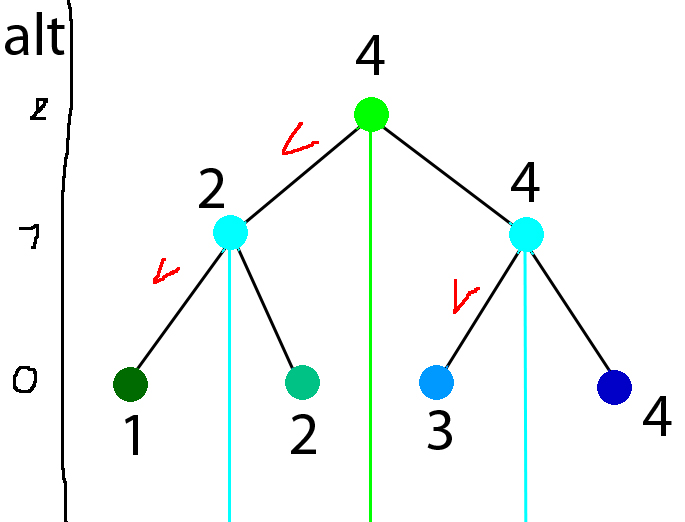
sur ce schéma les noeuds représentent les zones et non plus les salles
Pour bien lire cet arbre binaire : les noeuds sont des zones ; les feuilles (en bas) sont les zones minimales ; une zone comporte un ensemble de salles ; un noeud non-feuille a pour salles les salles de ses deux fils.
Vu qu'on a besoin de l'altitude pour donner une valeur à chaque zone, cela doit se faire une fois que l'algorithme de division du donjon est terminé.
On peut maintenant dire si une zone se trouve avant un blocage, et donc y mettre l'objet résolvant.
L'objet résolvant doit donc être placé dans une zone minimale :
- à la valeur inférieure strictement à celle de son blocage
- qui est un fils gauche.
Pour aller plus loin 2 : les cycles et les passages à sens unique
L'arbre est le squelette du donjon. Il est maintenant possible, pour rendre le donjon plus naturel, d'y ajouter des cycles.
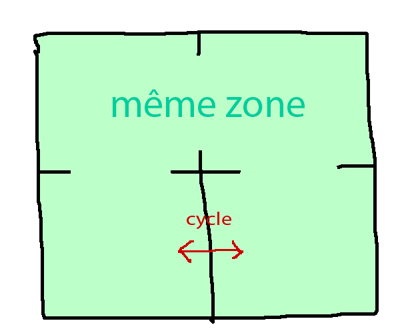
Ajout d'un cycle
La présence de cycles rend le donjon plus facile. J'aurais donc tendance à déconseiller le cycle, qui provoque l'inutilité de certaines salles du donjon. Donnez à ce phénomène une faible probabilité.
Si deux salles sont :
- géographiquement côte-à-côte (une coordonnée en commun, et l'autre coordonnée diffère de 1)
- séparées par un mur
- dans la même zone minimale (considérer les feuilles)
Alors on a le droit d'ouvrir le mur.
Respecter ces règles est très important pour ne pas quitter la structure du donjon décidée pendant l'algorithme.
Ajout d'un passage à sens unique :
Peut être utilisé pour :
- rendre le donjon plus labyrinthique
- permettre au joueur de revenir facilement dans les premières zones du donjon
Si deux salles sont :
- géographiquement côte-à-côte (une coordonnée en commun, et l'autre coordonnée diffère de 1)
- séparées par un mur
- la zone minimale (considérer les feuilles) de la salle A est avant (ou égale à) la zone minimale de la salle B
Alors on peut faire un chemin à sens unique allant de B vers A.
Respecter ces règles est très important pour ne pas quitter la structure du donjon décidée pendant l'algorithme. Le non-respect de ces règles peut déboucher sur un donjon infaisable !
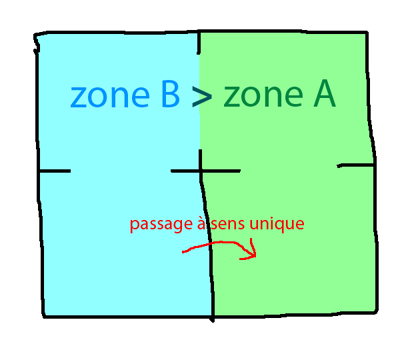
Le passage à sens unique peut être modélisé par une porte qui se referme juste derrière le héros, ou encore par la possibilité de sauter d'une petite falaise qui empêche de remonter.
J'aurais tendance à davantage préconiser le passage à sens unique par rapport au cycle.
Pour aller plus loin 3 : pouvoir forcément accéder à tout le donjon
Certains l'auront remarqué, le donjon exemple qui sert à expliquer l'algorithme peut être résolu de plusieurs façons différentes. Il est notamment possible d'utiliser la première clé pour accéder directement à la deuxième moitié du donjon (bleue), sans avoir à faire le deuxième quart du donjon (vert clair). Il est alors possible de finir le donjon sans pouvoir jamais visiter le deuxième quart du donjon.
Ce phénomène sera d'autant plus fréquent qu'on n'utilisera pas le "Pour aller plus loin 1".
Ce phénomène sera d'autant plus fréquent qu'on n'alternera pas la nature des blocages (serrure, porte qui s'ouvre grâce à un interrupteur, énigme impossible à résoudre sans l'arme du donjon...).
Pour corriger ce problème, il suffit d'ajouter les clés manquantes dans la toute dernière zone du donjon. Ainsi, quand le joueur aura fini le donjon, il pourra toujours revenir en arrière pour explorer les salles qu'il a évitées.
C'est la solution utilisée par le donjon-designer de Zelda Link's Awakening dans le cadre du donjon 3. Ce donjon, la "cave aux clés", peut être terminé sans avoir exploré plusieurs zones situées derrière des serrures. A la fin du donjon, le donjon-designer offre au joueur des clés pour lui permettre d'aller explorer ces zones facultatives du donjon. Le joueur se retrouve alors forcément avec des clés en trop une fois le donjon totalement exploré.
Si le fait d'avoir des clés en trop à la fin du donjon vous dérange, vous pouvez faire en sorte que les coffres ne donnent plus de clés une fois que toutes les portes du donjon ont été ouvertes. Remplacez par exemple les clés par un objet bonus inutile.
Pour aller plus loin 4 : salles subdivisées
La grande force des donjons de Zelda Link's Awakening est la subdivision des salles de ses donjons. J'entends par là que très souvent la salle est découpée en deux (ou plus !) zones hermétiques.

En quoi est-ce important ?
Cette simple caractéristique augmente considérablement le plaisir de résolution du donjon à partir d'un phénomène psychologique bien connu en game-design. Le joueur, en arrivant dans une salle subdivisée, aperçoit la zone de la salle à laquelle il ne peut pas accéder. Dans cette zone pour le moment inatteignable se trouve peut-être même un coffre ou d'autres bonus. Cela va créer un micro-but chez le joueur. La frustration de ne pas pouvoir accéder immédiatement à cette zone qu'on lui montre va faire qu'il va chercher à y aller.
Ce bête phénomène est le moteur principal de l'exploration ; le joueur n'a pas de raison d'agir à la base, c'est donc au game-designer de lui donner des buts, et ceci est la façon la moins artificielle de mouvoir le joueur. Une façon artificielle étant par exemple de dire au joueur "il faut que tu ailles là-bas pour des raisons scénaristiques".
Les donjons du jeu Binding of Izaac ne possèdent pas cette caractéristique et en font à mon sens de bien piètres donjons par rapport à ceux de Link's Awakening.
Pour faire un donjon à salles subdivisées comme dans Link's Awakening, il suffit de générer un donjon 4 fois plus grand pour ensuite coller les salles 4 par 4 :

Comment obtenir l'arbre des salles du début ?
Pour obtenir l'arbre des salles reliées, je propose le mini-algorithme suivant.
On part d'une case qui sera une salle centrale du donjon.
Il y a alors 4 possibilités pour étendre notre donjon : en haut, en bas, à gauche, à droite. Donnons une probabilité de 1/4 à l'ouverture de ces murs :

Une fois le choix fait, notre donjon s'agrandit d'une salle.
Il y a maintenant 6 possibilités pour étendre notre donjon :
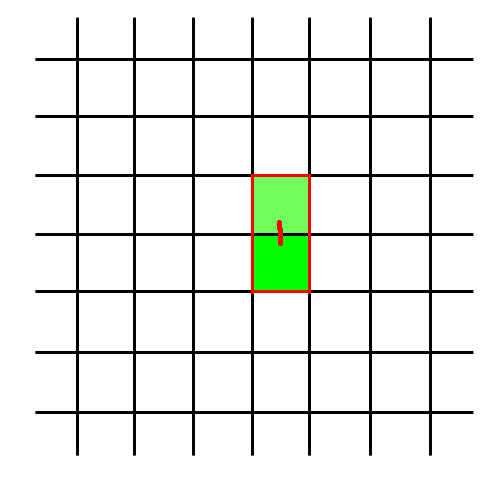
Faisons un choix avec une probabilité de 1/6 pour chaque mur externe :
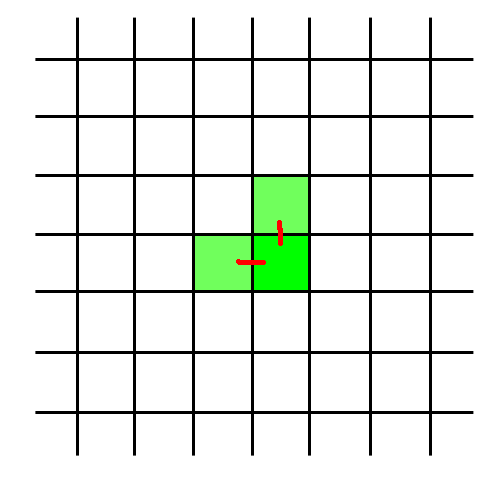
Je choisis de m'arrêter à un donjon de 12 salles :
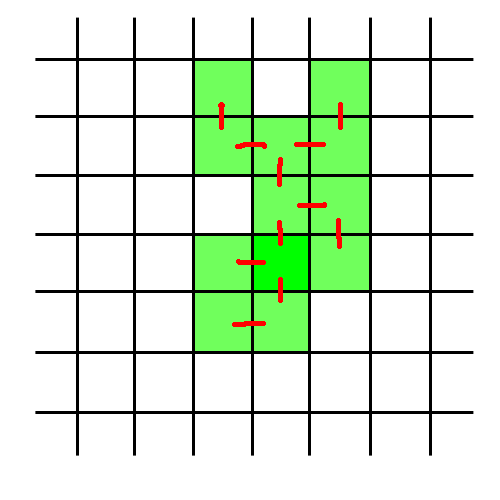
On peut choisir la forme globale du donjon à l'avance en fixant un contour que le donjon n'a pas le droit de dépasser durant son expansion. On demande alors à ce mini-algorithme exactement le nombre de salles de l'intérieur du contour limite.
Finalement, en appliquant le grand algorithme présenté au début de cet article, notre donjon devient :
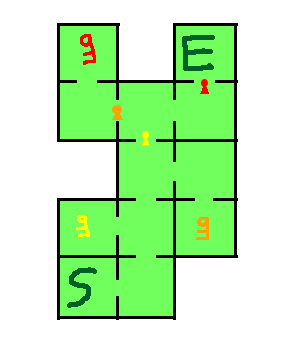
|

 Chat
Chat





































 -
-