
 Chat Chat |

|

Statistiques
Liste des
membres
Contact
Mentions légales
477 connectés actuellement
30732469 visiteurs
depuis l'ouverture
2448 visiteurs
aujourd'hui




Partenaires









Tous nos partenaires
Devenir
partenaire
Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306
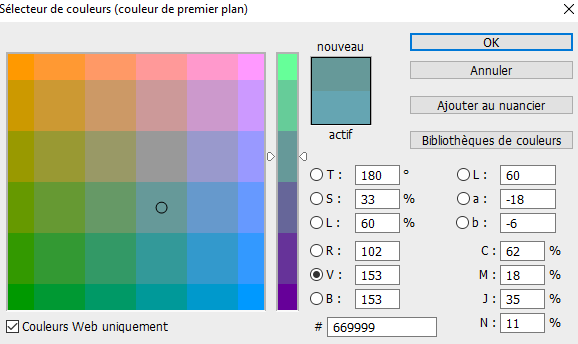
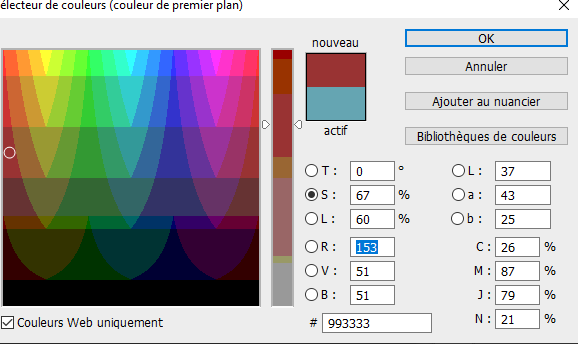
Reprise du message précédent: ❤ 0 Citoyen d'Alent En cliquant sur "couleurs web" dans la palette tu peux créer des palettes :
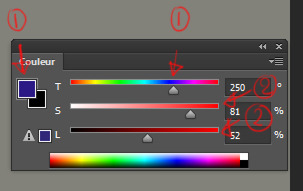
❤ 0 Indie game Developer Roi of the Suisse a dit: Bah avec Photoshop tu as les jauges HSL aussi, je ne vois pas le problème
❤ 1 Une vidéo super intéressante sur la façon dont Danton travaille : https://www.youtube.com/watch?v=McVHHDoPhdY
❤ 0 Indie game Developer Wow 85K abonnés sur Youtube, t'as percé Danton je savais pas ! Gg mec je vais suivre ta chaine ca a l'air hyper intéressant ❤ 0 C'est pas sa chaîne, il s'agit d'une interview. ^^'
❤ 0 Indie game Developer Oh my bad, c'est vrai que j'avais trouvé ça étrange de parler de soi à la 3ème personne, mais en général les artistes sont assez prétentieux donc ça m'a pas plus choqué que ça ❤ 5 ❤ 0 Chanter l'hyperchleuasme Très classe ! Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte ❤ 7 Bloqué dans la treizième dimension Un chien Spoiler (cliquez pour afficher)
www.dantonslip.com ❤ 0 Chanter l'hyperchleuasme Oh qu'il est beau Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte ❤ 0 Kawaii ! ❤ 0 On dirait bien que tu n'es plus sur l'aquarelle. C'est une commission ou un calendrier de l'Avent perso ? ❤ 0 Bloqué dans la treizième dimension Merci x)
Gari a dit: On dirait bien que tu n'es plus sur l'aquarelle. C'est une commission ou un calendrier de l'Avent perso ?
www.dantonslip.com ❤ 1 Vhehrhehn Y'a trop de level sur ce topic. Eldrao ~ PakuPaku ~ Winged Light ~ Ruin ~ Ma galerie ~ LTDAD ~ Don de graphismes plateforme 2D ❤ 10 Je suis toi Kuja vs djidane
❤ 0 Chanter l'hyperchleuasme Très chouette fanart de Djidane, le tripoteur de fesses Es-tu une star ? | Kujira no Hara | Muma|Rope | Polaris 03 | La 7e porte ❤ 0 Je suis toi pas la ref sorry
❤ 0 Narrer l'autocatégorème GG Raz. ❤ 1 Disciple de Pythagolf Je sais pas si ça a sa place ici mais voilà une petite animation extrait d'une vidéo que je prépare sur un truc de maths:
Spoiler (cliquez pour afficher)
~~ ❤ 0 Disciple de Pythagolf Nan sur de la géométrie convexe ^^ (le théorème de Helly plus précisément)
~~ ❤ 0 Citoyen d'Alent C'est propre ! J'ai été un peu perturbé par la façon dont les maisons se séparent, je saurais pas te dire pourquoi. ❤ 0 Bon, j'ai regardé sur l'ami wikipédia pour le théorème et la définition des convexes, et je crois avoir compris le fonctionnement (par contre je sais pas si c'est seulement avec trois convexes ou s'il peut y en avoir plus). Par contre il y a vraiment besoin de faire une animation pour ça ? (ça aurait pas été plus simple une série de schémas pour montrer différents cas ?)
❤ 0 Disciple de Pythagolf Citation: C'est propre ! J'ai été un peu perturbé par la façon dont les maisons se séparent, je saurais pas te dire pourquoi.
Citation: (par contre je sais pas si c'est seulement avec trois convexes ou s'il peut y en avoir plus)
Spoiler (cliquez pour afficher)
Citation:
~~ ❤ 0 Narrer l'autocatégorème GG. Oui les animations c'est important. Pour les gens comme qui ont une mémoire principalement visuelle (et qui sont très nuls maths ❤ 2 J'ai fait ça pour un santa secret !
Chromochimi (Arcade / Terminé) ||| La Question (Mini-jeu narratif / Terminé !) ||| Blade Converter (A-RPG ~ Beat them all / En cours !) ||| Des mini-projets Unity ! ❤ 7 Aller à la page 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 Index du forum > Vos créations > Bazar des créations !
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Merci de ne pas reproduire le contenu de ce site sans autorisation.
Contacter l'équipe - Mentions légales






 -
- 




 =>[]
=>[]












 -
- 


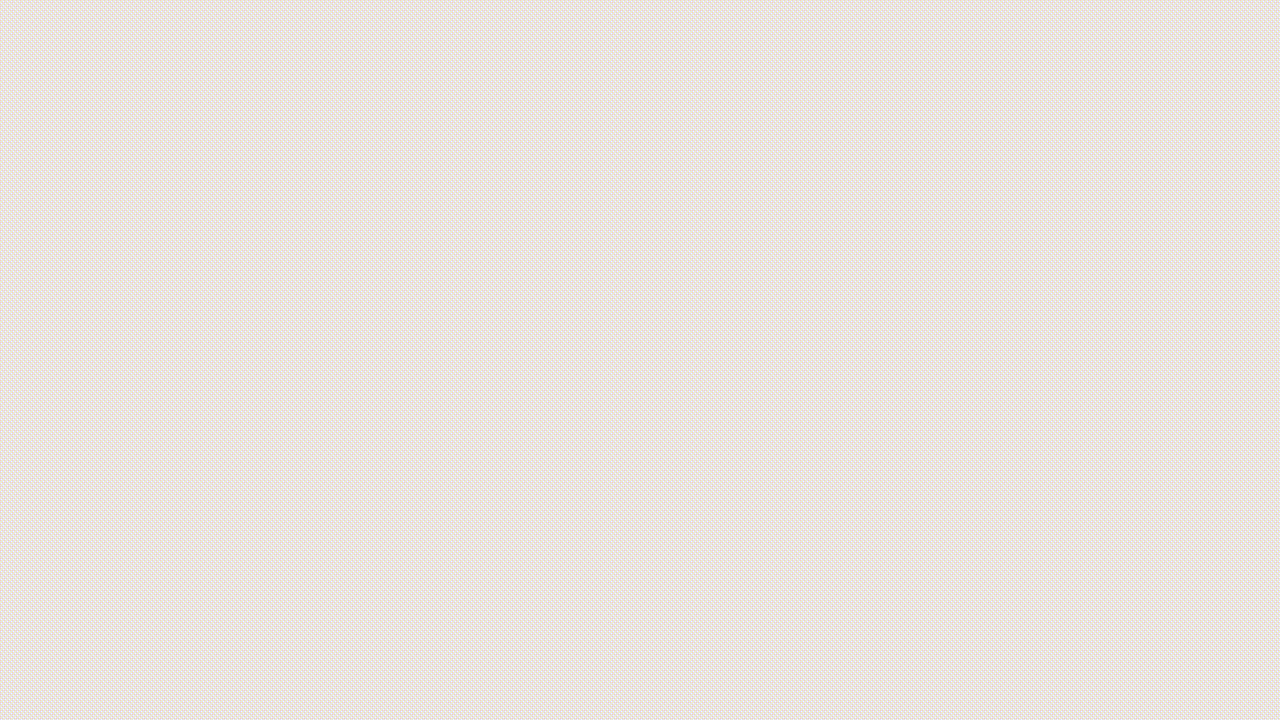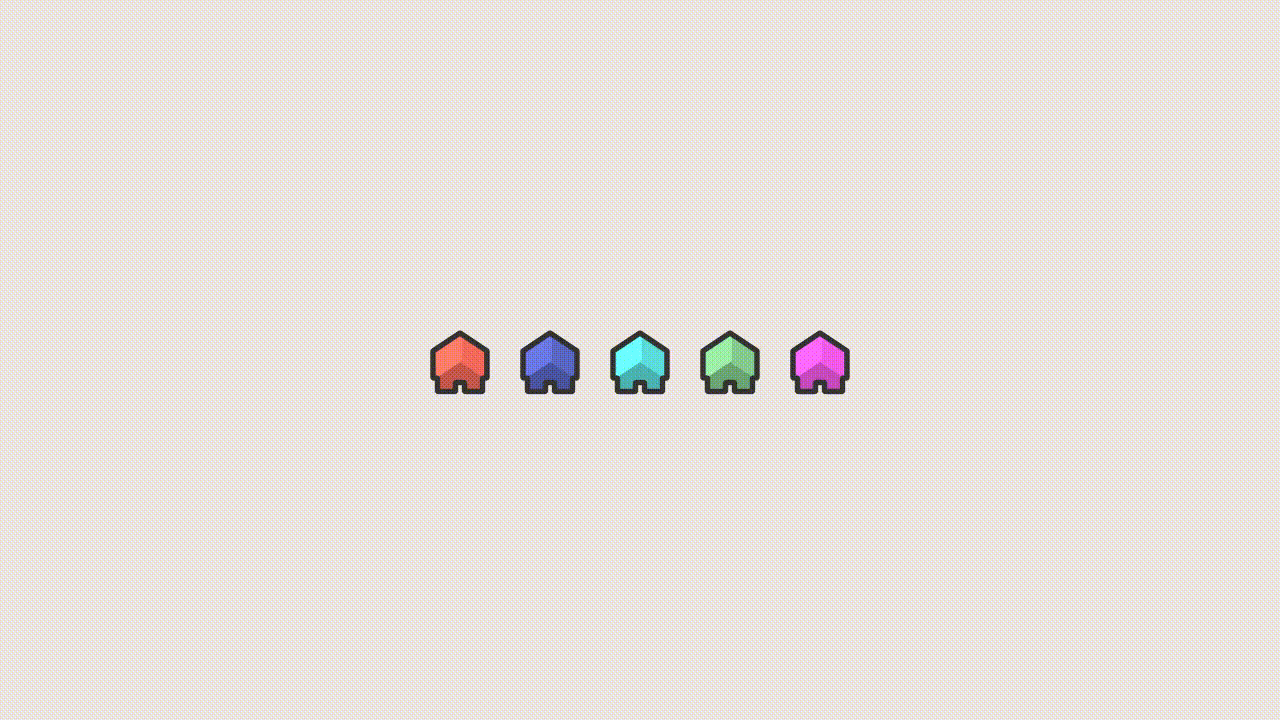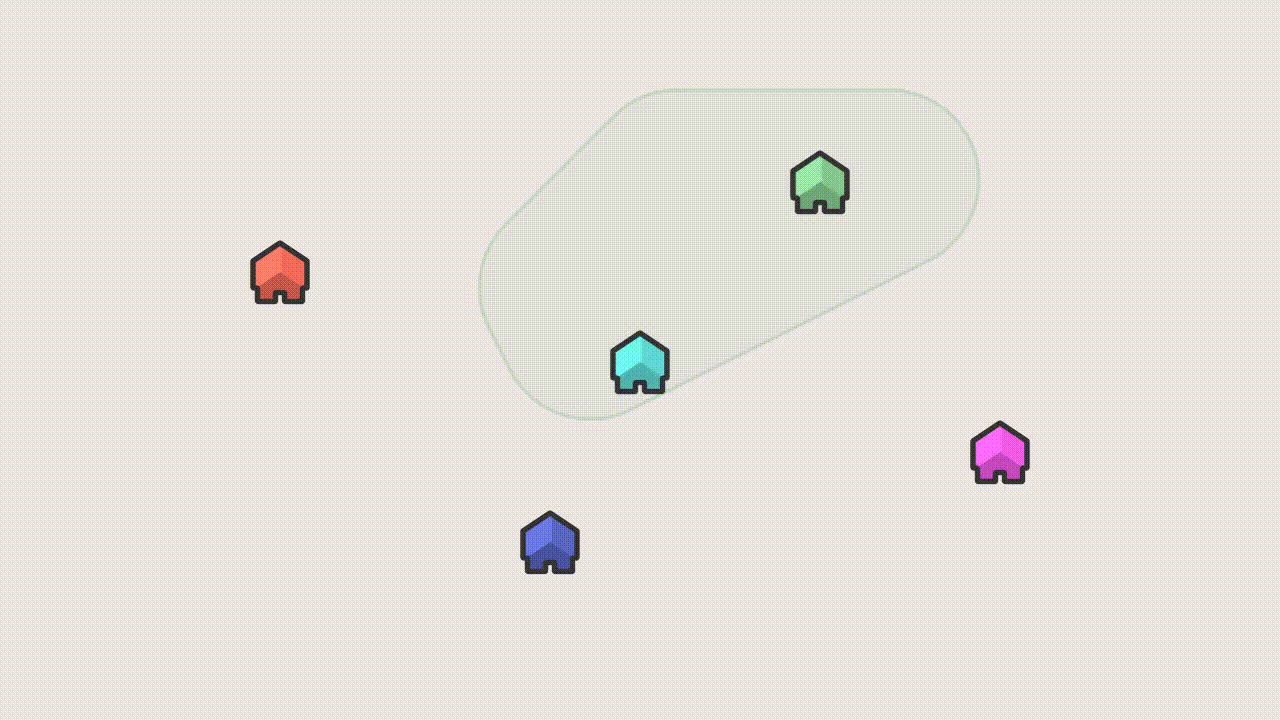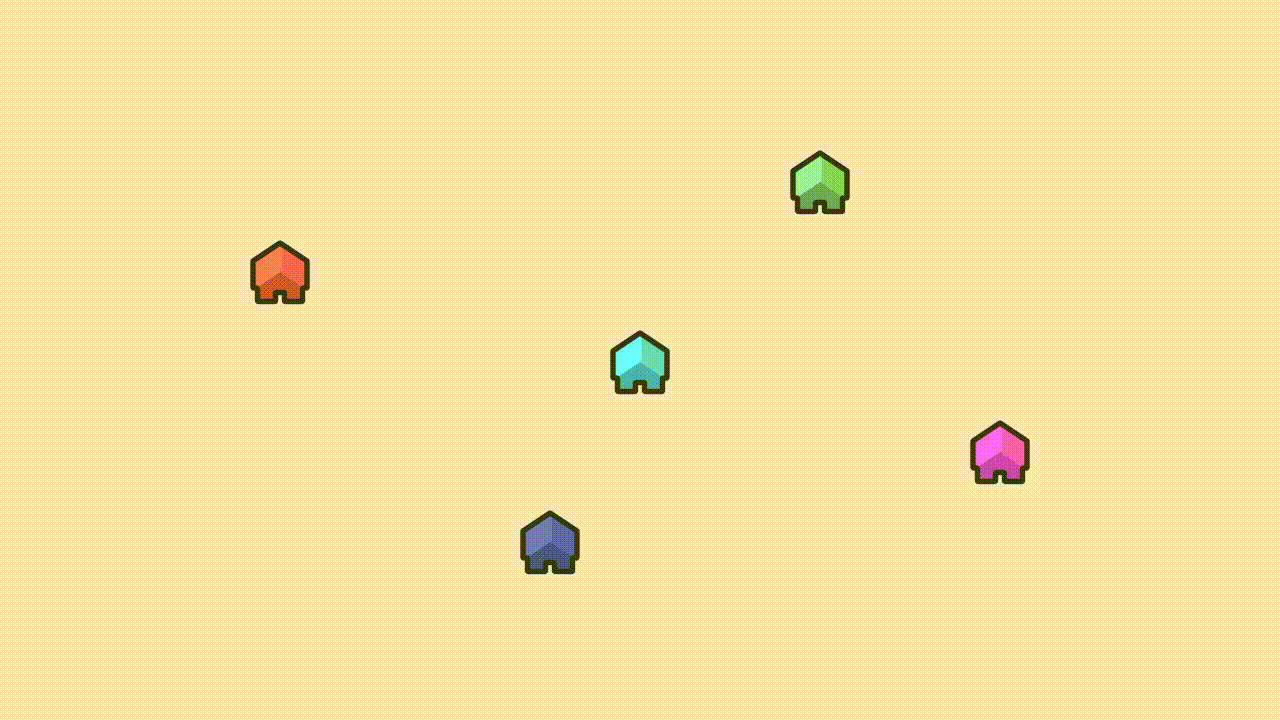
 ) ça aide bien.
) ça aide bien.



